Using Monte Carlo Simulation for Biomedical Device Design

Light from biomedical devices interacts with human tissue, which contains a variety of structures and cell sizes and shapes. In many cases, optical scattering plays a strong role in the propagation of optical radiation. One common approach to simulating scattering is the Monte Carlo technique.
Popular optics-simulation software incorporates Monte Carlo scattering, allowing you to circumvent the need to create your own code. However, a custom implementation allows for greater control of the simulation – and will certainly sharpen your understanding of how the technique works.
Monte Carlo simulations are probabilistic simulations of complex dynamics, usually with simplifying assumptions to make the computations more efficient. The Monte Carlo approach was introduced to physics by Ulam and von Neumann in the late 1940’s to explore neutron diffusion for the Manhattan Project. From that first use, Monte Carlo techniques spread to other areas of physics, other areas of science, and domains as diverse as telecommunications network design and finance.
In a bio-optical context, you can avoid an intractable calculation of wave propagation and interaction with multitudinous cells by simulating a large ensemble of photon-bunch trajectories. Each trajectory is broken into a number of segments. For each segment, microscopic calculation of the photons’ interaction with all the molecules in a region is replaced by a single random event, the probability of which is characterized by the average absorption and scattering probabilities for the tissue. At the end of the simulation, you can calculate the statistical properties of the ensemble of photon bunches, such as mean path length or probability that the trajectory passes through a detector.
In such an approach, photon interactions are classified into two discrete types: absorption and scattering. Absorption is characterized by the absorption coefficient ma representing Beer’s-law-type attenuation as the light propagates. Elastic scattering is quantified by the scattering coefficient ms, which represents the probability that the photon scatters.
A Monte-Carlo simulation keeps track of photon trajectory only, and not photon phase. A photon that scatters back into its pre-scatter direction of travel is indistinguishable from a photon that didn’t scatter at all. And most scattering off biological tissue is preferentially in the forward direction. Thus, in performing a Monte-Carlo simulation the “bare” scattering coefficient µs, is reduced to the effective scattering coefficient µs’ = µs(1 – g), in which the “geometry factor” g quantifies the fraction of scattering that occurs in the forward direction. The effective scattering coefficient tracks only those photons that have scattered out of the initial trajectory direction, and are thus distinguishable from unscattered photons.
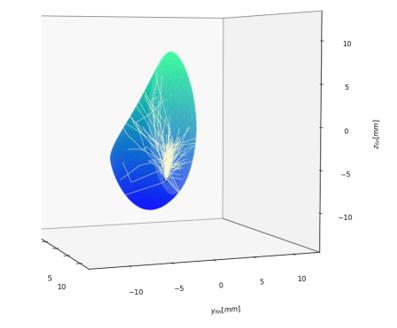
Consider the scattering of light in human breast tissue (see Figure 1): a situation relevant to mammography using diffuse optical tomography. To obtain a first estimate of probability of photon detection at a distant location, you might assume homogeneous breast tissue (aside from the possibility of an optically distinct tumor region). A Monte Carlo simulation follows the launch, propagation, and interactions (absorption/scattering) experienced by a photon bunch. The bunch is treated collectively: at each computational step the bunch either collectively survives, collectively exits, or – due to absorption – drops below the threshold for further tracking, and is collectively terminated. The simulation contains the following steps:
- Launch: A photon bunch with initial weight W0 is launched from the origin, either in a given direction (for a collimated source) or in a randomly chosen direction consistent with the numerical aperture of the source. The weight represents the probability that the bunch remains “alive,” and has not yet been terminated. The initial weight W0=1.0.
- Propagate: The bunch travels along its current trajectory a distance D drawn from an exponential probability distribution. The exponent is taken to be µtot = (µa + µs’): that is, the attenuation accounts both for photon absorption and scattering out of its current direction of propagation.Think of D as the distance the photon bunch travels before its next interaction. Using a randomly chosen propagation distance selected in this manner is a standard Monte Carlo “trick” used to ensure that the photon bunch is either collectively absorbed or collectively scattered on each step – no computational resources are used simulating “uninteresting” interaction-free propagation segments.
- Drop: After propagating the distance D, the photon-bunch weight W is reduced to W·(1 – Pa), where Pa is the probability that the interaction is an absorption, rather than elastic scattering:
Pa = µa /(µa + µs’). - Check exit: The trajectory is checked against the breast-boundary geometry to determine if the photons remaining in the bunch exit the breast on that step. If so, then the bunch is terminated. If the trajectory passes through the detector as it exits, and if the propagation direction falls within the acceptance angle of the detector, the bunch is flagged as “detected.” The final “detected weight” of the photon bunch at the detector is set to the current value of W, rather than to 1.The “number of detection events” may be non-integer, and is always less than the bare number of bunch trajectories that pass through the detector.
- Roulette: At this juncture, the “fate” of the photon bunch is assessed. The bunch’s current weight is compared to a threshold value (taken in the current simulations to be 0.01). If the weight falls below this threshold value, then: The bunch trajectory is terminated with some probability Pt.
Otherwise, the weight is multiplied (increased) by 1/Pt, and the bunch continues to the next iteration.
This methodology is a “variance reduction technique,” standard in Monte Carlo simulations (Kahn, “Random sampling Monte Carlo techniques in neutron attenuation problems I,” Nucleonics, 6, 27, 1950 and Kahn, “Random sampling Monte Carlo techniques in neutron attenuation problems II,” Nucleonics, 6, 61, 1950). - Spin: Before going to the next iteration, the photon bunch’s propagation direction is randomly updated, according to the geometry factor g, using the Henyey-Greenstein scattering function probability distribution (Henyey, Greenstein, “Diffuse radiation in the galaxy,” Astrophysical Journal 93, 70, 1941):
The Henyey Greenstein scattering function describes the average value of the cosine of the angular change in propagation direction upon scattering, and is used as a simple parametrization of the complete and complex microscopic scattering distribution. Its use is standard in the simulation of scattering in biological tissue[1].
For a given photon bunch, steps two through six are iterated until the bunch is terminated. Repeat the process for a large number of bunches (perhaps as many as 105 to 107) to statistically estimate quantities of interest.
The Monte Carlo technique is a useful arrow to have in your quiver when you’re analyzing the interactions between light and the human body. It provides a complementary perspective to classical raytracing, or coherent propagation/diffraction calculations. A “prototypical” implementation of Monte Carlo for biological tissue is the MC321 code (by Steven L. Jacques, listed at OMLC.org), which can be a useful waypoint when implementing your own Monte Carlo light scattering code.
Further discussion of Monte Carlo simulation in the context of tissue light scattering may be found, for example, in the PhD thesis of Scott Prahl (“Light Transport in Tissue,” U. Texas at Austin).
[1] If ξ is a uniform probability distribution on the interval (0,1], you may obtain the above p(cosθ) by drawing from ξ according to:
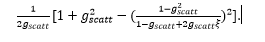
Brian King isPrincipal Optical Systems Engineer at StarFish Medical. Previously Manager of Optical Engineering and Systems Engineering at Cymer Semiconductor, Brian was an Assistant Professor at McMaster University. Brian holds a B.Sc in Mathematical Physics from SFU, and an M.S. and Ph.D. in Physics from the University of Colorado at Boulder.
Roulette wheel Image Credit: ID 9778153 © Tomas Hajek | Dreamstime.com