Creep analyses are often required in the design of products. One difficulty in performing a creep analysis is that it generally involves a non-linear approach demanding a high-end simulation package or package add-on. In addition, a non-linear analysis employing a modeling technique like the Bailey-Norton law requires creep constants that are often difficult to find. Medical devices are usually designed with healthy safety factors and are often not as tightly space constrained or mass constrained as the ultra-miniature world of cell phone design. It is for these reasons, that a simpler approach to creep analysis rendering slightly larger and or heavier design solutions can provide viable results with less cost in some situations.

A linear approach to providing a conservative analysis of a part where creep is a concern can be realized by referencing the effective elastic modulus at the temperature and time interval of interest. Often this is 50°C and 5 years, i.e., the service temperature limit and the product life. In figure 12, Delrin’s stress strain curve is plotted with iso-curves of different duration at 45°C. The curves are not linear for long exposures; however, connecting the end points of the 50,000 hr curve and calculating the elastic modulus is conservative. These types of curves are easier to find in the literature than creep constants for specific materials and are certainly available for generic classes of thermoplastics.

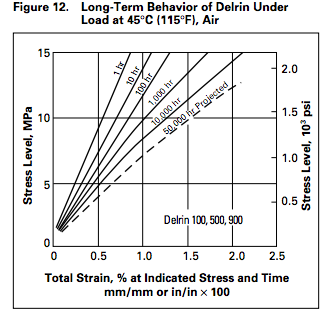
A traditional linear FEA can then be conducted on the part in question using this “downgraded” elastic modulus. Deflections predicted by the analysis will be a reasonable conservative estimate of the likely end-of-life deflections due to creep. Another analysis with the traditional modulus can be conducted to determine the creep effects vs. the standard load induced deflections. Often there are other graphs with different exposure temperatures allowing interpolation to the desired temperature.

In situations where the time-history of the creep is important, where the temperature and environmental conditions vacillate, where the loading fluctuates or when one is designing for a low safety factor where absolute minimal size and weight are paramount; a more thorough treatment is required and advocated. It is in situations where the ultimate worst-case movement due to creep is of interest that a simple linear analysis can save the designer a great deal of time and resources.