An example of are moulded plastic light guides, an inexpensive means to “pipe” light around inside a medical device. Their design process makes light guides amenable to a variety of shapes and sizes.  Coupling Light from LEDs and Light Guides applications include delivering light to an indicator, a switch, or a peripheral diagnostic attachment. These optical guides are an attractive technology for solving a light-transport problem in a medical device.

The performance capabilities of such a “light conduit” can only be realized if light can be successfully coupled into the conduit in the first place! One can imagine a never-ending succession of Rube-Golberg-like optical schemes to accomplish this goal. In practice, the number of efficient schemes is actually quite limited. In this blog, I’ll discuss several of these schemes and why other strategies will have more limited success in coupling light from LEDs and light guides.

Coupling Light from LEDs and light guides (also called “light pipes”) work through total internal reflection (TIR). If light travels from a material with a higher index of refraction to one with a lower index, and the angle of incidence ϴ_wall on the interface exceeds a critical angle , then 100% of the light is reflected off the interface, and back into the interior of the first material (see Figure 1). Such a surface makes an ideal “mirror.” In principle, light inside such a light guide will be reflected from one end of the guide to the other without loss – barring changes in guide geometry (e.g. bends, scratches) or absorption in the guide material.

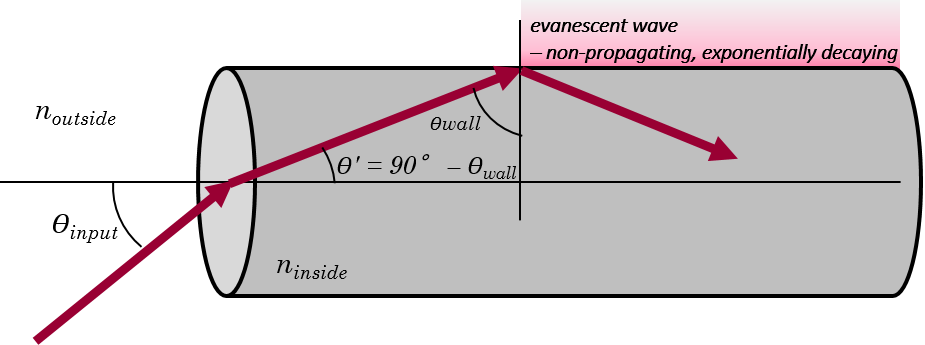
Figure 1: geometry of a light guide. n_outside < n_inside.

As a prelude to the following discussion, it’s worthwhile thinking about how Snell’s law of refraction pertains to light leaving an LED, and to light entering the light guide.

1. Light leaving the LED: the index of refraction of LED materials ranges from 2.5 (InGaN, blue/green) to almost 4 for NIR LEDs. As light passes from the semiconductor bulk into the air, 2 effects occur:
   2. For angles greater than the critical angle (slightly less than 24° for n=2.5 and slightly less than 15° for n=3.95), the light attempting to exit the semiconductor experiences total internal reflection and fails to make it to the outside world. Such rays are absorbed internally into the LED material, and generally are a significant source of heat.
   3. For light rays that do make it out of the semiconductor, their direction of propagation is bent towards the surface of the semiconductor. Rays near the critical angle are bent to almost 90°, that is, nearly parallel to the surface of the emitter!

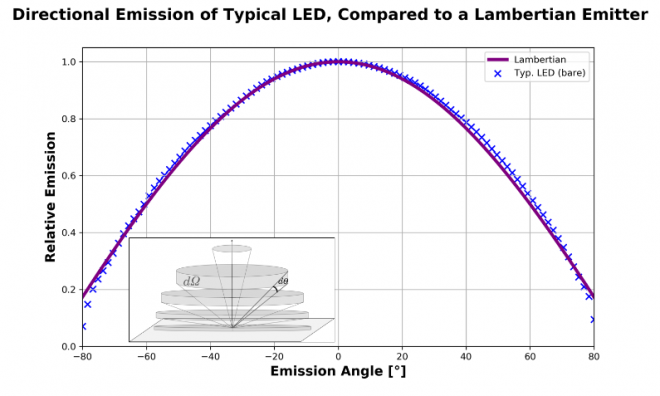
Since semiconductors are epitaxially grown, almost all LED emitters will have a flat face. Therefore, LEDs generically tend to internally capture a substantial portion of their optical output and to send what light does escape in all directions up to ±90°. Further, for most LEDs, this angular spread is mostly uniform: that is, the LED is a good approximation to a Lambertian emitter (see Figure 2), and the angular distribution of light is pretty much as uniform as it can be in 3D space. Catching this light and directing it somewhere can pose a challenge.

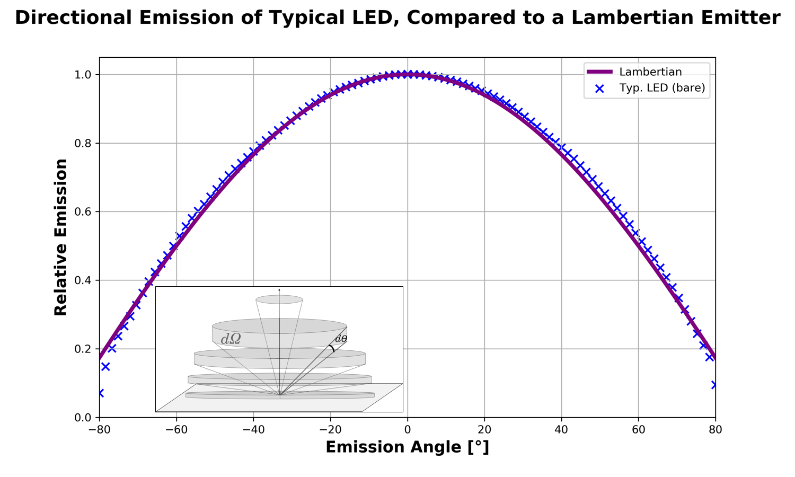
Figure 2: The angular-emission pattern of a typical bare-chip LED, compared to an ideal (“Lambertian”) emitter that radiates uniformly into all directions of the hemisphere. The agreement is quite striking. (Note: The falloff with angle is due to the increase in surface area of a unit sphere as the direction moves from being directly overhead to more aligned with the cut-plane of the hemisphere – see inset.)

Some LED manufacturers immerse the semiconductor in a flat or curved epoxy layer, whose index of refraction is intermediate between that of the semiconductor and that of air. This epoxy somewhat reduces reflection losses but doesn’t fundamentally change the circumstances. In the cases in which this layer is curved, it acts as a first lens in the optical system – and the general discussion of lenses below still pertains.

2. Light entering the light guide: For typical moldable, optically transparent plastics, and a light guide in air whose entrance face is perpendicular to its sidewalls, rays striking the input face at any angle are bent at the interface such that they experience TIR at the walls of the guide. That is: any light passing through the light guide’s entrance face undergoes TIR inside the guide. (This statement would be true even if the guide were fashioned out of specialty “low-index” plastics with, e.g. n as low as 1.37.)

Although LEDs are particularly awful at producing directed light, light guides are particularly indiscriminate in their acceptance of “poorly directed” light.

However, though light guides’ acceptance angle is large, the size of their entrance face is always limited to some extent. And – regardless of propagation angle – a ray of light can only enter the light guide if it actually hits the entrance face![1]

Hence, the general guideline for maximal coupling of light into light guides: put the light-guide entrance face as close as possible to the LED output face. That way, the light guide entrance subtends the largest-possible (solid-) angle as seen from the LED output face – the LED light “sees light guide no matter which way it looks…” An optical designer may be tempted to put a lens in between the LED and the light guide to enhance the amount of light coupled in. There may be good reasons to interpose a lens (for example, to make a more-collimated far-field beam at the light-guide exit). However, in terms of coupling efficiency, this generally hurts: it effectively moves the light-guide further from the LED, thus reducing the fraction of light it can capture.

I’ll discuss these nuances in two cases: in which the light-guide entrance is larger than the LED exit face, and in which the LED exit face is larger than the light-guide entrance.

1. Light guide entrance face larger than LED:
   In some circumstances, it may not be possible to place the light-guide entrance close to the LED, either due to routing constraints or perhaps due to concerns about parasitic LED heat melting the plastic. In this case, a lens may be used to capture a portion of the escaping LED light and redirect it to the light-guide entrance.I’ll assume the lens is bigger than the light-guide entrance face, to capture as much light as possible. If the lens is negative, then it generally increases the divergence of the ray-bundle it intercepts – resulting in less light hitting the light-guide than would have in absence of the lens. A positive lens yields the same result if the LED is located inside the lens’s focal distance f. Thus, neither of these situations is a good idea in terms of capturing the most light.

Figure 3: Passing light from an LED through a simple positive lens, as the location d_LED of the LED is varied with respect to the LED position. (a) If the LED lies inside the lens’s focal distance f, then the light rays from the LED diverge after the lens. A similar situation results if the positive lens is replaced by a negative one. (b) If the LED lies between f and 2f from the lens, a magnified real image of the LED is formed on the far side of the lens. (c) If the LED lies further than 2f from the lens, a de-magnified image is formed, a distance d_image that is further from the lens than is f.

On the other hand, if the LED is located a distance from the lens that lies between f and 2f, a magnified image of the LED is created on the other side of the lens. In this situation, if the magnified image is larger than the Iight-guide entrance aperture, light is lost.

Since the minimum extent of the ray bundle occurs at the image location, that is the optimal location for the light-guide entrance face[2] in terms of coupling efficiency. The transverse magnification of the image M_T is given by M_T = d_i/d_LED = f /(d_LED – f ), where d_LED is the distance from the LED to the lens, and d_i is the distance from the lens to the image of the LED. Thus, if the LED has transverse extent D_LED and the light guide has transverse extent D_LG, the closest the LED may be brought to the lens without some of the LED image falling outside the light-guide entrance is
d_closest = f (1 + D_LED/D_LG).

This is an important consideration: at the end of the day, the lens is – at best – sending all the light that strikes it to the light-guide entrance. But that’s all it can send! So the further the lens from the LED, the less LED light it captures in the first place. Another way to think of the above formula is that if the lens can be no closer than d_closest due to some design constraint, then (a) the lens should be chosen to be as large as possible, to intercept as much light as possible, and (b) the focal length of the lens should be chosen such that f  = d_closest/(1 + D_LED/D_LG). One might imagine more complex, multi-lens designs to escape this constraint. However, because most LEDs’ output is fundamentally distributed uniformly in all directions, such designs will still miss the light that would otherwise be captured by simply moving the light guide entrance up to the LED[3].

Similarly, if the LED is located farther than 2f from the lens, a smaller-than-life image of the LED is created on the other side of the lens. The light guide entrance face may be placed anywhere the converging (or post-image diverging) bundle of rays is of a smaller extent than the light guide image. On the other hand, in this scenario, the lens captures less light than it otherwise could, which is non-optimal.

In the above discussion, I was assuming a plano-convex or biconvex lens. A more attractive option would be a positive-power meniscus lens – such a lens can “wrap around” the LED, thus capturing more light. This is what LED manufacturers often do – in so-called “lensed LEDs.” The lens creates a magnified image of the LED – but a magnified image implies a lowering of ray-bundle divergence, as Figure 3 shows. Thus, the LED output may be more collimated than for a bare emitter.

There’s one more coupling light from LEDs and light guides configuration – used by LED manufacturers – that’s worth discussing: one in which the lens material encases the LED emitter. None of the above considerations are different. However – and this is key – if the light from the LED leaves the semiconductor entering into a material with a higher index than air, the critical angle is increased and more light can escape the semiconductor. If the other side of the higher-index material (e.g. epoxy) has positive curvature, the angle of incidence onto the air interface can be reduced, thus reducing the Fresnel losses at that surface as well.

1. LED larger than light guide:
   This is the scenario in which optical designers may run the risk of wrapping themselves around the axle when trying to maximize throughput. The reason is the temptation to try to couple more light into the light guide than one could simply by butting the light guide up against the LED. However, the fundamental advice remains the same: put the light-guide entrance face as close as possible to the LED output face.One may be tempted to buy a lensed LED or to use a lens to try to demagnify the LED image until the whole LED surface is imaged into the light-guide face. But the above advice still holds: if the lens is external to the LED assembly, demagnification only occurs if the lens is further than 2f from the emitter surface – and the rays emitted by the LED in that case are spreading out all the way as they travel to the lens! You’d do better to remove the lens and move the light-guide entrance up to the LED. For more complicated optical designs that mitigate the lens-placement constraint for a single lens, the demagnification is accompanied by a proportional increase in divergence angles of the light. Given the divergence of the LED light itself, this invariably means that some of the light will escape the optical system on the way to the light-guide entrance. Similarly, if you buy an LED with the emitter encased in a lens material, the light rays are diverging all the way to the lens-air surface. Slightly more rays make it into the lens in the first place, but you’ll still probably be better off by selecting the unlensed variety and moving the light guide right up to the emitter surface[4].

Most of the above discussion can be captured by a concept known as conservation of etendue – which states that the product of the angular extent of a ray bundle and its cross-sectional area is unchanged by any optical element. The inherently high angular extent of light from LEDs causes optical designs to tend to run aground in this conservation principle. However, that would be the subject of a whole other blog! In the meantime, just remember that to maximize coupling light from LEDs and light guides in medical devices, put the light-guide entrance face as close as possible to the LED output face.