Computational modeling thermoplastic properties to predict or validate thermoplastic properties in medical device design is essential for effective design and optimization of thermoplastic parts and products in medical device products. Their non-linear material properties play a critical role in performance and behavior.

During setup of computational modeling thermoplastic properties, these factors should be top of mind to predict and validate thermoplastic behaviour in the real-world implementation of medical devices. Disregarding these effects can have drastic consequences in predictive models’ accuracy. 

Selecting the correct material for a medical device or component helps ensure an effective and robust product. In patient-contacting medical applications, polymers are the material of choice. They have a large advantage over metals as the salinity and acidity of humans’ skin degrades metals, whereas high-molecular weight polymers are quite resistant. They are also robust, chemically resistant for sanitation, able to be textured, and lightweight. If you walk through a modern hospital, you will come across many examples of thermoplastics in medical devices, including hospital beds, MRI and CT machines, ultrasound carts, and consumables like syringes, drapes, and patient gowns. 

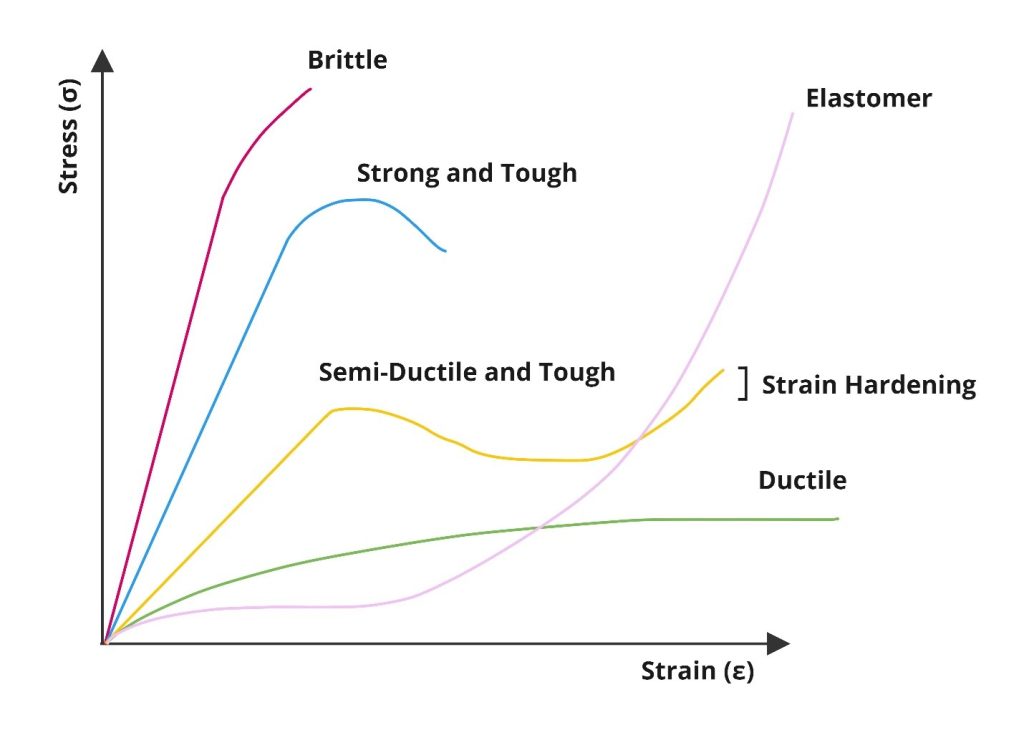
Thermoplastics’ behaviour is unique from other materials due to their molecular structure. Typically, molecules are lengthy and amorphous in orientation, adjusting to stress in a rate-dependent manner. Strain rate also has a large influence on stress-strain response, demonstrated in contrasting between drops/impacts and material relaxation over time (e.g., self-threading fasteners in thermoplastics).  

The range of behaviours is shown in Figure 1, where classes of thermoplastics have been organized to visualize behavioural response examples. 

A topical example is given by an amorphous sample of nylon, aka polyamide, a frequently used semi-ductile and tough thermoplastic. A tensile stress-strain graph is shown in Figure 2 (left side). On the application of force, the initial response is linear until a short nonlinear region begins. Then yield occurs, plastically deforming the material permanently. Further strain leads to necking and strain softening, which is a reduction in stress due to plastic deformation and a reorientation of the amorphous polymer into an oriented microstructure.  

Thermoplastics are made up of long chains of repeating molecular units, known as monomers. These monomers are linked together through chemical bonds, forming a three-dimensional network of interconnected chains. The molecular structure of thermoplastics plays a significant role in their non-linear material properties. Given the example of a gradual application of stress on nylon, if the necking region is allowed to reorient its molecules into a crystalline structure due to the stress response, strain hardening then begins. A visual, stepwise demonstration of this necking and reorientation process is shown in Figure 2 (right side). With continued force applied, and at an adequately high rate, the material will fail resulting in a break-line and separation – this is called ultimate tensile failure. 

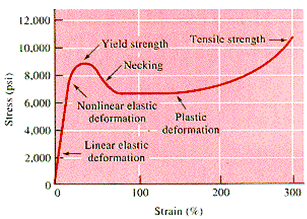
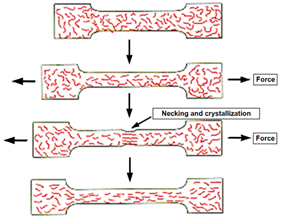
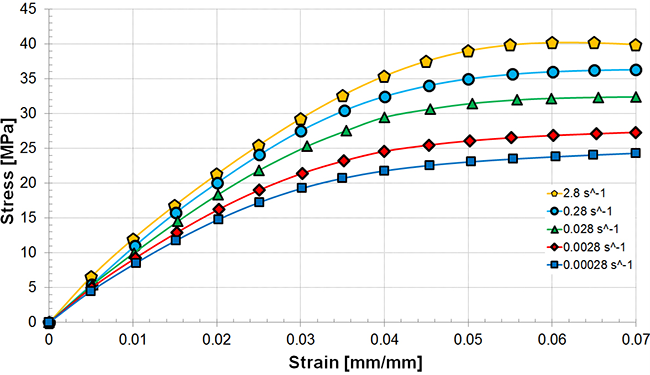
Figure 2 shows stress-strain and molecular response at a fixed strain rate. However, when strain rate varies so does the stress response. As above, a slow application rate can allow for linearization of molecules and therefore a strain softening reduction in stress. The faster strain is applied, the less the molecules can flow to adapt, and therefore the stress response becomes higher.  

This is shown in Figure 3, where at 7% strain (a rate difference of 4 orders of magnitude) the stress is increased by almost a factor of 2. This can become a factor depending on the application of stress. Consider the difference between an impact such as dropping an object vs. a slow change such as thermal cycling over a region with residual stress (e.g., welded-interface plastic enclosure). This strain rate sensitivity can have significant implications for the design and performance of thermoplastic parts as it affects their strength, toughness, and impact resistance. 

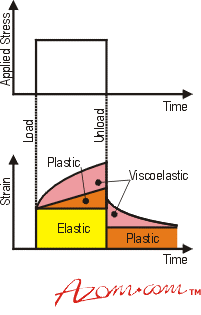
While the above describes how strain rate can show differences over strain %, it’s also important to consider the underlying time-dependencies and nonlinearities inherent in thermoplastics. Thermoplastics’ response to applied stress can be described as a stacked response over time, including elastic, plastic, and viscoelastic responses. 

Review Figure 4 – given an adequate applied stress, plastic will also exhibit a sizable viscoelastic response in addition to elastic and plastic deformation. The time-dependency exists due to molecular reorientation as in the previous figure. If held, it will eventually level-off to a strain that represents equilibrium. But if stress is removed, then plastic deformation is retained, and the viscoelastic portion of strain relieves non-linearly over time. Over stress-strain cycles, this presents itself as hysteresis.

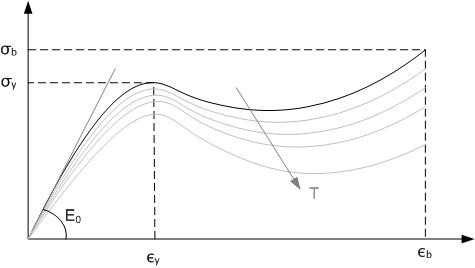
Thermoplastics also exhibit non-linear behavior in terms of their temperature-dependent properties. Review Figure 5 to visualize how this affects material strength. As the temperature of a thermoplastic increases, its material properties change, becoming more viscoelastic and less brittle. This can be observed in the temperature-dependent modulus of elasticity and the glass transition temperature, which are both important parameters in the design and analysis of thermoplastic parts.

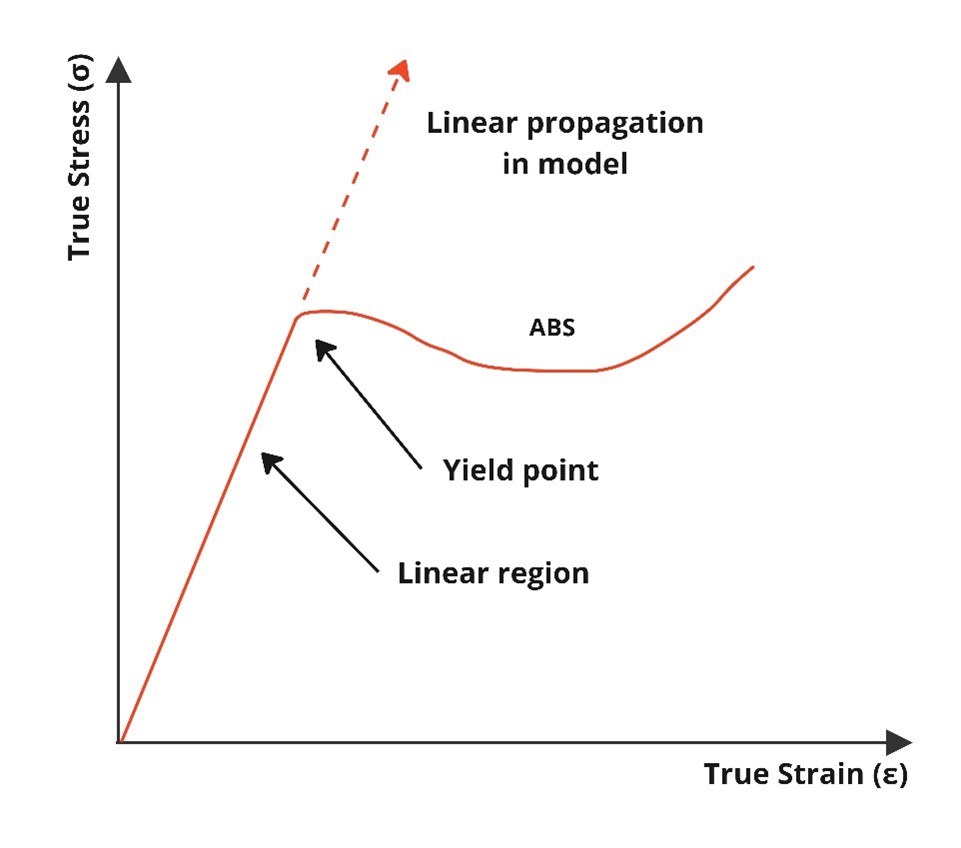
As stated earlier, there are cases when linear material properties would be adequate for a computational modeling analysis, such as when any plastic deformation is unacceptable. However, this would only be useful to detect local impact regions’ yield onset in say, a drop test, with no meaningful accuracy beyond that point. This is demonstrated by Figure 6 – the dashed line beyond the yield point shows comparatively very little strain and wouldn’t present any of the plastic deformation present in material experiencing the non-linear solid region. If propagation of plastic effects or failure modeling are important in an analysis, test data that includes elastic, plastic, ultimate failure, and consideration for rate-dependency should be included as inputs. 

Predicting or validating these properties and understanding their influence and importance in design is essential for the development of thermoplastic-inclusive components and products. Whether using computational modeling or physical prototypes, keep these factors top of mind when testing and deploying real-world medical devices that include thermoplastics.